|
Last week I worked error propagation for a pitot measurement to flow rate conversion.
Because it's a measurement, there is a natural level of precision that we can only estimate that depends on the precision level of each of our measuring points (our tools). Yet, we (maybe just I) often overlooked the concept of measurement error. In this tool (below), I've incorporated the error propagation to suggest a range for the result instead of what we typically express as a near-certain test measurement. So, now, you can convert a pitot pressure into a flow rate and immediately get the error tolerance based on the tools you've used and measurements you've taken. Hardly any additional work. While it may sound trivial, knowing what amount of tolerance we are actually achieving in a test measurement could be the difference between a test pass or test failure - especially in regards to fire pump testing. Check out the tool below, and let me know what you think! It has an IP and SI version built in (I'm finally catching on).
If you're a member of MeyerFire University this will be added to the iOS and Android app automatically.
Thanks and have a great rest of your week! - Joe When you conduct a hydrant flow test, how precise is your resulting measurement? Let’s say a flow test summary shows 82 psi static, 54 psi residual at 956 gpm. Is it really 956 gpm? Well, no, of course – but 956 is the best resulting estimate of the flow test with the information and measurements we have at hand. It’s where the dial best predicts. But how precise is that measurement, really? Are we certain that it’s 956 gpm and not 957 gpm, or 960 gpm, or 1,000 gpm? Now of course, a hydrant flow test is a point-in-time measurement. It’s not representative of daily fluctuation or seasonal fluctuation. Let’s save that discussion for another time. What I’m really interested in is when we take a flow test or run a pump test, how accurate are our results, really? SIGNIFICANT DIGITS The concept of significant digits is one simple way avoid suggesting a higher level of precision than a measurement justifies. In other words, if our flow test results said 956.21 gpm, we’re suggesting, based on the decimal placement that we actually know that the value is not 956.4 gpm; it’s instead between 956.2 and 956.3. That’s a level of precision that is suggested by significant digits. Technically, if we had a pitot gauge reading of 9 psi during a flow test, then we would have one significant digit. Using one significant digit is very problematic in flow test results. Q=29.84×C×d²×√P In this flow conversion formula above (the Freeman Flow Formula), we take we take pitot pressure (P), opening diameter (d), and the Coefficient of Discharge (C), to get a resulting estimate of flow through an opening. The problem with using the significant concept is that a pitot reading of a single digit value would mean that we round our resulting flow would yield one significant digit. LOW PITOT MEASUREMENT NFPA 291 actually recommends that pitot readings less than 10 psi should be avoided, if possible. That would mean flowing fewer outlets to get a higher pitot reading to avoid inaccurate readings. So, at least in theory, three 2.5” outlets with a C-factor of 0.90 and a pitot of 9 psi each would result in a flow estimate of 1,511 gpm being rounded to – what – 1,000 gpm or 2,000 gpm? The concept of ‘significant digits’ here would result in massive rounding error. This line of logic is where I was really curious about our flow test results – or really any measurement of flow, such as pump testing. How precise are our measurements? BIG GAUGES, SMALL TICKMARKS If you’ve tried to take a close reading and nitpick the difference between 96 and 97 psi on a 300 psi gauge – that can be extremely difficult to do. Yet, at least in the case of fire pump testing, that result can be the difference between passing or failing a fire pump test. How precise can we read a higher-range gauge with small or grouped tickmarks and a small-diameter face? If you don’t think that’s a high-stakes proposition, then I’d invite you to wrap up final acceptance testing on a federal project with every stakeholder present and watching. It can be high stakes. Perhaps the more appropriate way to understand precision is by doing error propagation on this conversion. Error propagation is a sore point for me, as I pretty much failed every physics lab in college that required it. Time to shed those demons. If you’re not into math, skip ahead to the summary to see where I ended up. I want to show my work here as I haven’t seen this done and I’m very much for transparency and getting feedback, especially when I venture a little beyond my own fenceposts. ERROR PROPAGATION FOR FLOW TEST CONVERSION Error propagation is a fancy way to describe the reliability of the resulting calculation. How precise is the result? That’s what we want to know – and knowing so can help us make more informed decisions in our assessments. A formula with multiple variables, where each have their own uncertainty, the overall uncertainty depends upon how each variable affects the final result. In other words – if I’m not exactly sure about the numbers I’m putting in, how unsure should I be about the answer I get out? IMPACT OF DIAMETER VS. PITOT PRESSURE In this equation, a percentage error in measurement of a diameter could have an outsized effect on the resulting flow since diameter is squared. To run an error propagation on a formula involving variables which are multiplied together, we square the relative uncertainty (change in a measurement divided by the measurement), square them, add them together, and square out the result. EXAMPLE: 60 PSI GAUGE So, let’s say we ran a flow test where we were certain in the Coefficient of Discharge (0.90), we measured and were confident in the diameter of 2.5 inches (within a 1/16th of an inch), and took a pitot reading of two side outlets each at 8 psi using a 60 psi gauge with 1% accuracy. Practically speaking, that’s a very reasonable amount of tolerance of a normal hydrant flow test or fire pump test. With those results, we would calculate a total flow estimate of about 950 gpm. How precise is that flow? (Error in flow test reading measuring opening within 1/16” and pitot with 60 psi gauge) So, with a variation of + 59 gpm, our resulting flow estimate would be 950 gpm + 59 gpm, or a resulting range of between 890 gpm and 1010 gpm. That’s a pretty wide variation – and it’s certainly a lot wider than I would have expected considering we’re using a 60 psi gauge with 1% accuracy. EXAMPLE: 100 PSI GAUGE What would happen if we used a 100 psi gauge with 1% accuracy? (Error in flow test reading measuring opening within 1/16” and pitot with 100 psi gauge) EXAMPLE: 300 PSI GAUGE Taken to an extreme – what if we used a 300 psi gauge to measure pitot? A bad idea for sure (it’s nearly impossible to read sensitive low amounts, and likely in the least-accurate portion of the gauge. But just for kicks: (Error in flow test reading measuring opening within 1/16” and pitot with 300 psi gauge - which we would never recommend doing) EXAMPLE: 60 PSI GAUGE WITH IMPRECISE DIAMETER Now, what if we were less confident in the actual inside diameter of the hydrant side outlet? What if we thought it was 2.5”, but only within an 1/8th of an inch? With our 60 psi gauge: (Error in flow test reading measuring opening within 1/8” and pitot with 60 psi gauge) Yikes! Did you notice that? Even with a 60 psi gauge, if we only know the inside diameter within an 1/8th of an inch, it’s worse than using a 100 psi gauge. Knowing the precise inside diameter is important as it has a huge effect on the level of precision. HOW DO WE IMPROVE PRECISION? Based on the inputs – there are a few key ways to improve the precision of flow test readings when we use pitot gauges to estimate the amount of flow. I’m interested in writing more on this in the coming weeks, but there are a number of ways in which we can improve the precision of our flow testing and have more confidence in our results. #1 MEASURE THE OPENING SIZE First – and probably the most important based on our calculation – is to know the exact diameter of the orifice opening. If we are flowing out the side of an outlet, we actually need to measure, with precision, the inside diameter of that opening. As I’ve been told, not all inside diameters are equal. They depend on the exact make and model of a hydrant. I’ve made this mistake before and assumed all 2.5” side outlets are the same inside diameter. To improve precision, take a careful measurement of the exact inside diameter of the opening down to the 1/16th of an inch. Alternatively, using a factory-created attachment with a factory-milled opening will help define and make that variation go away. A known diameter with a very tight factory tolerance helps us reduce or eliminate this concern altogether. #2 USE SMALLER RANGE GAUGES In general, we want to use the smallest range for the gauge possible. Using a 300 psi gauge to measure anything within 0-30 psi is problematic. Not only is that a less-accurate range for a gauge (near the ends), it’s extremely difficult to read. The tickmarks just become too small to read well. Instead, we want to use the lowest gauge range that’s possible for the test. If we’re expecting results below 100 psi, can we use a 100 psi gauge instead of 200 or 300? If we’re measuring pitot and expecting values under 60, can we use a 60 psi gauge? Even a 30 psi gauge? The bigger the tickmarks and the smaller the range, the better we’re going to be able to see and read the results. Using a lower-range scale gauge can lead to far-easier reading of the gauge, but also be within a more accurate range for the gauge itself. #3 LARGER-DIAMETER GAUGES
This goes against my “travel with small things” concept, but larger-diameter gauge faces are so much easier to read in the field. They cost more. They’re bigger. But man are they easier to pull values from. Again – on an important fire pump closeout with many people all watching – having nice clear results to prove the system works as it should helps. #4 USE CALIBRATED GAUGES For fire pump testing, NFPA 20 requires that all gauges undergo annual calibration testing and be accurate within 1 percent. (NFPA 20-2022 Section 14.2.6.1.2) For fire hydrant flow tests, that same mandate doesn’t necessarily apply. NFPA 291 is a recommended practice, and requires calibration within 12 months, but is not necessarily enforceable in the same way that NFPA 20 is. Now, if you’re on a federal project and NFPA 291’s “shoulds” become “shalls”, then there are enforceable teeth. But for private practice work, many flow tests are simply run with whatever gauge is on the truck that day. Using a calibrated gauge will obviously hone in for more precise measurement. #5 USE STREAM-STRAIGHTENERS NFPA 291 now specifically states a preference for playpipes or stream straighteners to improve the accuracy of readings. Not only do these address the precise opening sizes we talked about earlier, but they hold the pitot measurements in a fixed-in-place mounting position. This also means we should be measuring at exactly the right center-of-stream location. This is explicitly listed now in NFPA 291 (2022) Section 4.6.2. SUMMARY Doing a little error propagation highlights a few things about the measurement process in a calculated way. We can look at the accuracy of our input measurements an in turn, get a level of confidence about the resulting range of flow from those measurements. The more precise we are able to measure, the more confidence we have in the result – which is both an obvious ‘gut-feeling’ but can also be mathematically proven. YOUR TAKE I’m interested in your take. What are your tips for more accurate readings? What stories do you have about fire pump acceptance testing or hydrant flow tests in this regard? NEXT STEPS I’d like to venture down this rabbit hole just a little further. My next thought is to apply the error propagation concept into a quick calculator tool where you could see your error range yourself – and experiment with different situations. You might just find an error range based on your normal test equipment that could present your test results in a more appropriate and transparent way. That's TBD (to be developed). Thanks for reading – and, as always, for fighting the good fight. Have a great rest of your week. - Joe
On the MeyerFire University side of things we've been getting into the fundamentals of hydraulic calculations and the basis for how we perform calculations today.
One of the concepts that I had not explored in any kind of detail was the Hazen-Williams formula itself - outside of perhaps a few hand calculations here or there when studying for a NICET or the PE Exam. It was developed early 20th center by Gardner Williams and Allen Hazen when they studied records of friction loss measurements from a range of experimenters. The formula they derived was empirical. For hydraulic calculations - it's been the staple our industry and the basis behind our systems today. I'd be particularly interested in diving a little deeper than we typically would to get a job done, and that might come in posts here in the next few weeks. How do we reduce pressure loss in our systems? What does the actual construction of the formula tell us about flow in our system? WHAT THE FORMULA SUGGESTS The exponents here are relevant - because of that 1.85 exponent - if we double our flow, then our pressure loss increases by 260%. If we triple our flow, then the pressure loss is 7.6 times the original! Exponents affect the C-Factor too. If our C-Factor improves from 100 to 120, our pressure loss drops 29%. What applications could that have for us? Well, if we install nitrogen on a new dry system - our C-Factor goes from 100 to 120. That could be a big deal on the right projects. What about diameter? With the 4.87 exponent, that has the biggest effect of all. If our diameter doubles, our pressure loss drops 97%! Even going from 2-inch to 2.5-inch drops pressure loss by about 60%! Of the variables in the Hazen-Williams equation, diameter has the greatest impact on friction loss. HYDRAULIC PARALYSIS We know that intuitively as pipe diameter is our first go-to for solving hydraulic issues and is also the one element we have the most control over as a designer. One concept not to gloss over, though, is the pipe schedule. Even seemingly minor differences in pipe schedule (thickness) can have a major effect on pressure loss considering that the effects of diameter have an exponential effect on pressure loss. If you're banging your head against a wall trying to round out a hydraulic calculation, make sure that all of your pipe diameters are optimized (of course), but also check that your pipe schedule is accurate. The difference between a Schedule 40 and Schedule 10 calculation over a long enough distance and a sensitive-enough portion of the calculation could have a big effect on pressure loss. Also - if you're ever stuck - try our tipsheet on ways to get out of a jam (Article #1 and Cheatsheet #2). In experimenting around with different values, I went ahead and put together a small calculator that does a Hazen Williams calculation with a few helpful lookup tables already included. If you don't see the tool below, click to check it out:
If you're well into your career, this might not present a whole lot of practical need - any sprinkler hydraulic calculation program already has this incorporated of course.
What I wanted to do is simply break out the calculation to explore the effects in a little more detail. Take the sample calculation, and tweak the inputs just a bit - you can do so by clicking on a dropdown, making any selection, then use the up/down arrows on your keyboard to flip through values quickly. YOUR TAKE What do you see that people often miss about the Hazen Williams formula? What, if anything, would you want to see on this tool as a means of learning about the fundamentals? I think it would be a little interesting to start a dialogue on the limits of Hazen Williams and potential range of accuracy (that is, actually explore it mathematically and possibly disprove some of the frustrating assumptions that tend to pop up regularly). What do you want to see? Water velocity? Limits? Comparison to Darcy-Weisbach? Let me know below. Hope to nerd out a little and see what we can come up with together. |
ALL-ACCESSSUBSCRIBEGet Free Articles via Email:
+ Get calculators, tools, resources and articles
+ Get our PDF Flowchart for Canopy & Overhang Requirements instantly + No spam
+ Unsubscribe anytime AUTHORJoe Meyer, PE, is a Fire Protection Engineer out of St. Louis, Missouri who writes & develops resources for Fire Protection Professionals. See bio here: About FILTERS
All
ARCHIVES
July 2024
|
MeyerFire
- Blog
- Forum
-
THE TOOLKIT
- SUBMIT AN IDEA
- BACKFLOW DATABASE*
- CLEAN AGENT ESTIMATOR*
- CLOUD CEILING CALCULATOR
- DOMESTIC DEMAND*
- FIRE FLOW CALCULATOR*
- FIRE PUMP ANALYZER*
- FIRE PUMP DATABASE*
- FRICTION LOSS CALCULATOR
- HANGER SPACER*
- IBC TRANSLATOR*
- K-FACTOR SELECTOR*
- NFPA 13 EDITION TRANSLATOR ('19 ONLY)
- NFPA 13 EDITION TRANSLATOR ('99-'22)*
- LIQUIDS ANALYZER*
- OBSTRUCTION CALCULATOR
- OBSTRUCTIONS AGAINST WALL*
- PITOT CONVERTER
- PLUMBING FIXTURE COUNTS
- QUICK RESPONSE AREA REDUCTION
- REMOTE AREA ANALYZER*
- SPRINKLER DATABASE*
- SPRINKLER FLOW*
- SYSTEM ESTIMATOR*
- TEST & DRAIN CALCULATOR
- THRUST BLOCK CALCULATOR
- TRAPEZE CALCULATOR
- UNIT CONVERTER
- VOLUME & COMPRESSOR CALCULATOR
- WATER STORAGE*
- WATER SUPPLY (US)
- WATER SUPPLY (METRIC)
- UNIVERSITY
- PE Exam
- LOGIN
- PRICING
- OUR CAUSE

MeyerFire.com is a startup community built to help fire protection professionals shine.
Our goal is to improve fire protection practices worldwide. We promote the industry by creating helpful tools and resources, and by bringing together industry professionals to share their expertise.
MeyerFire, LLC is a NICET Recognized Training Provider and International Code Council Preferred Education Provider.
All text, images, and media Copyright © 2016-2024 MeyerFire, LLC
We respect your privacy and personal data. See our Privacy Policy and Terms of Service. The views, opinions, and information found on this site represent solely the author and do not represent the opinions of any other party, nor does the presented material assume responsibility for its use. Fire protection and life safety systems constitute a critical component for public health and safety and you should consult with a licensed professional for proper design and code adherence.
Discussions are solely for the purpose of peer review and the exchange of ideas. All comments are reviewed. Comments which do not contribute, are not relevant, are spam, or are disrespectful in nature may be removed. Information presented and opinions expressed should not be relied upon as a replacement for consulting services. Some (not all) outbound links on this website, such as Amazon links, are affiliate-based where we receive a small commission for orders placed elsewhere.



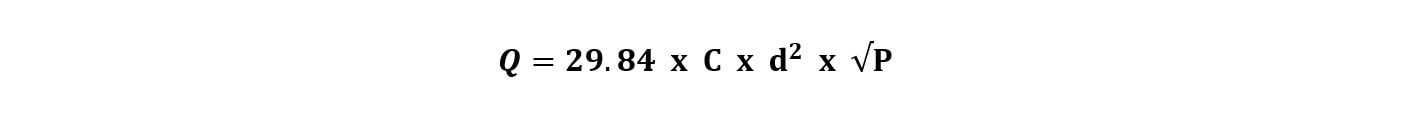
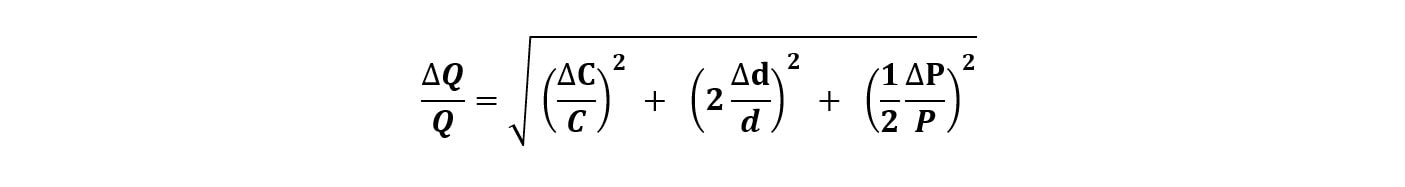
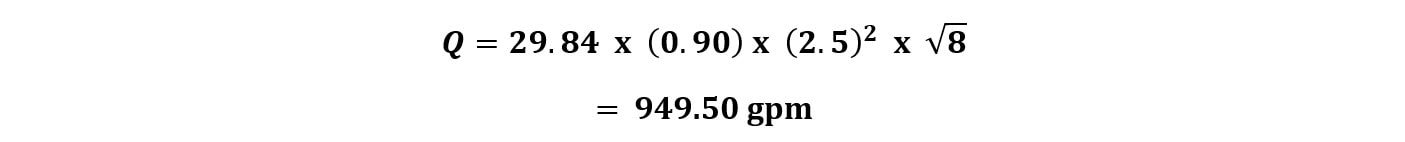

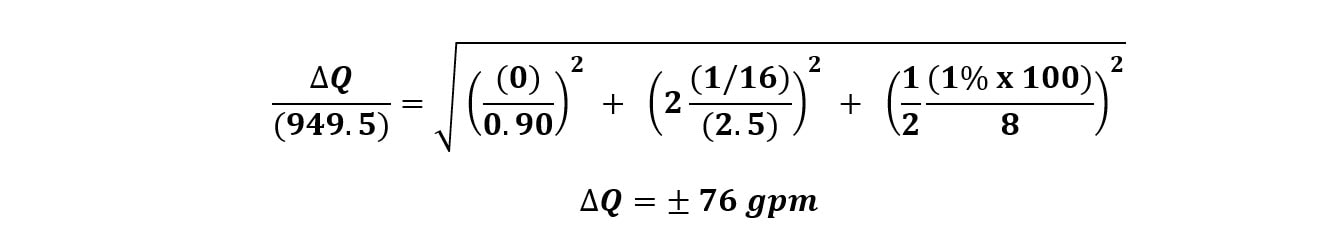
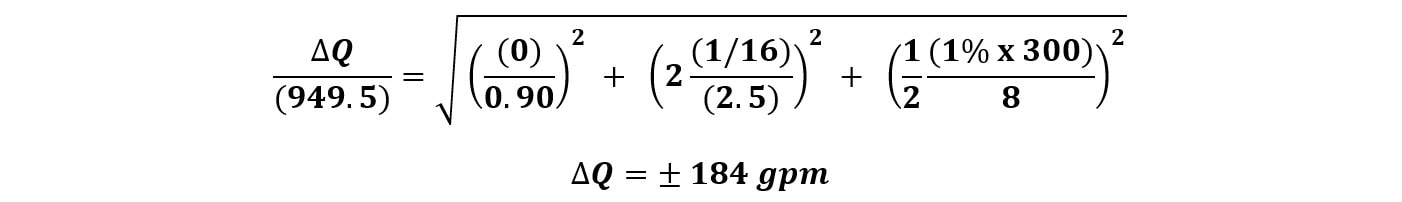
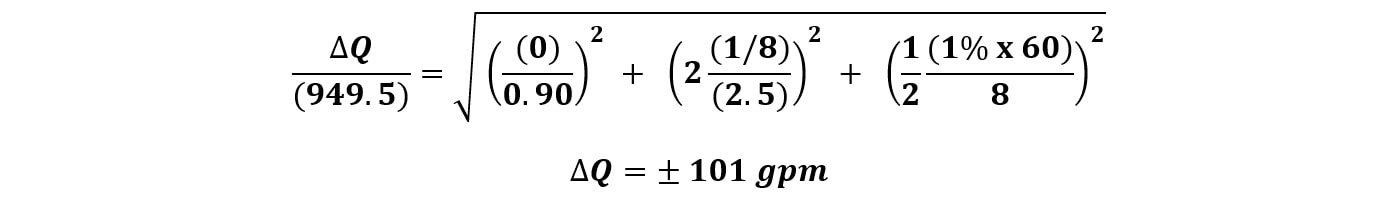

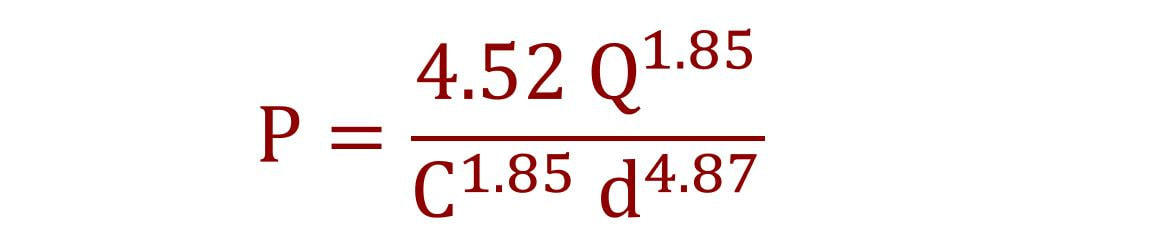



 RSS Feed
RSS Feed
